版权声明：署名，答应他人基于本文举行创作，且必须基于与原先答应协议雷同的答应协议分发本文 （Creative Commons）

什么是二叉搜索树

二叉搜索树（Binary Search Tree），（又名：二叉查找树、二叉排序树）它大概是一棵空树。是一种特殊的二叉树，具有以下性子：

• 若它的左子树不为空，则左子树上全部节点的值都小于根结点的值。
• 若它的右子树不为空，则右子树上全部节点的值都大于根节点的值。
• 它的左右子树也分别为二叉搜索树。

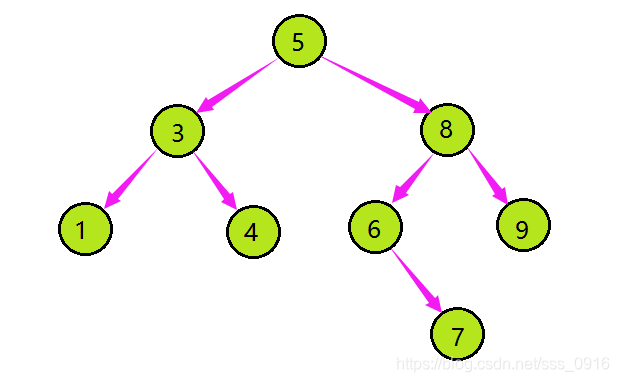
二叉搜索树原理：
二叉搜索树的查找过程和二叉树雷同，通常接纳二叉链作为二叉搜索树的存储布局。中序遍历二叉搜索树可以可到一个关键字的有序序列；一个无需序列可以通过构造一棵二叉搜索树变成一个有序序列，构造树的过程即为对无需序枚举行排序的过程。每次插入的新节点都是二叉搜索树上新的叶子节点，在举行插入操纵时，不必移动其他节点，只须要改动某个节点的指针，由空变为非空即可。二叉搜索树搜索、插入、删除的复杂度便是树高，O(log(n))。

二叉搜索树的操纵

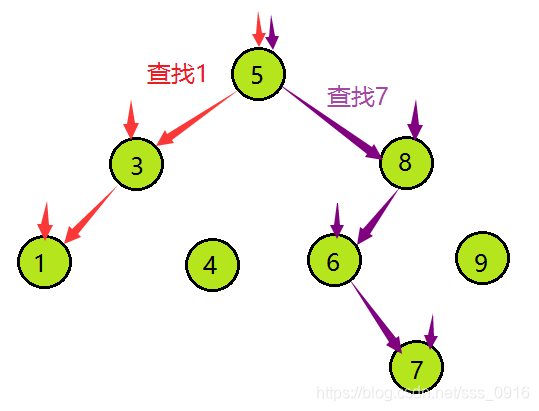
二叉搜索树的查找：

• 若根节点不为空：
  假如根节点key==查找的key，返回true；
  假如根节点key>查找的key，在其左子树查找；
  假如根节点key<查找的key，在其右子树查找；
• 若根节点为空，返回false；

二叉树的插入：
插入的过程如下：

1. 假如树为空，则直接插入，然后返回true。
   
2. 树不为空，按二叉搜索树的性子查找插入位置，插入新节点。
   

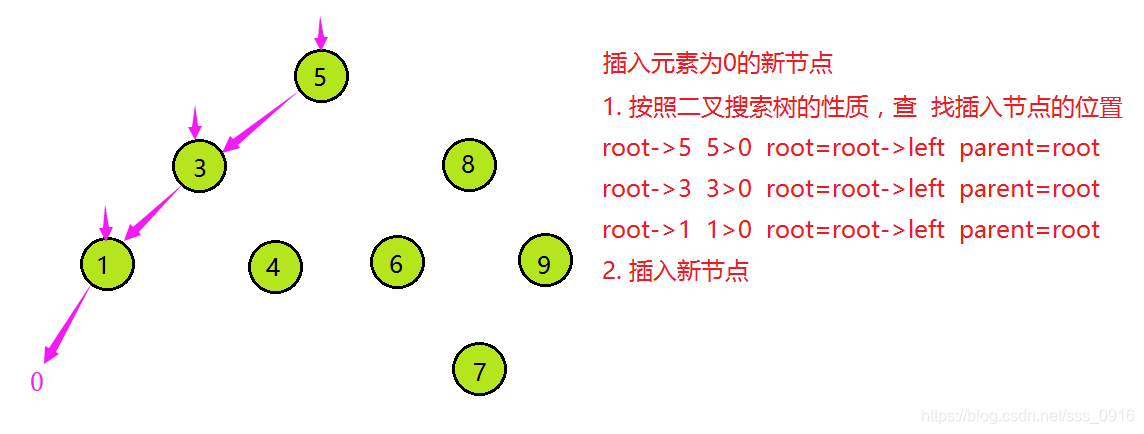
二叉搜索树的删除：
起首查找元素是否在二叉搜索树中，假如不存在，则返回，否则要删除的结点大概分下面四种环境：

1. 要删除的结点无孩子结点；
2. 要删除的结点只有左孩子结点；
3. 要删除的结点只有右孩子结点；
4. 要删除的结点有左、右孩子结点；

看似有四种环境，第一种可以和第二种或第三种归并起来，总结如下：

• 只有左孩子，删除该节点且使被删除结点的双亲结点指向被删除结点的左孩子结点。
• 只有右孩子，删除该节点且使被删除结点的双亲结点指向被删除结点的右孩子结点。
• 有左右孩子，在它的右子树中探求中序下的第一个结点（关键码最小），用它的值弥补到被删除结点中，再来处理处罚该节点的删除题目。

二叉搜索树性能分析

插入和删除操纵都必须先查找，查找服从代表了二叉搜索树中各个操纵的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相称，则二叉搜索树匀称查找长度是结点在二叉搜索树深度的函数，即结点越深，比力次数越多。
但对于同一个键值聚集，假如各键值插入的序次差异，大概得到差异布局的二叉搜索树。

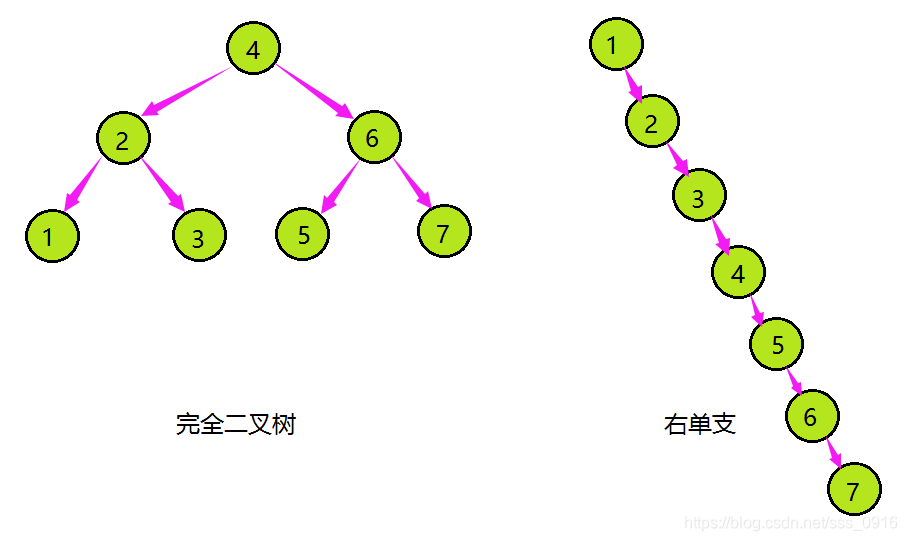
• 最优环境下，二叉搜索树为完全二叉树，匀称比力次数为：log2(N)；
• 最差环境下，二叉搜索树退化为单支树，匀称比力次数为：N/2；

假如退化成单支树，二叉搜索树的性能就失去了。这就是二叉搜索树的题目所在。有没有什么改进的方法呢？有，但是这里就不先容了。可以提一下：AVL树。

模拟实现二叉搜索树

模拟实现中碰到的题目：

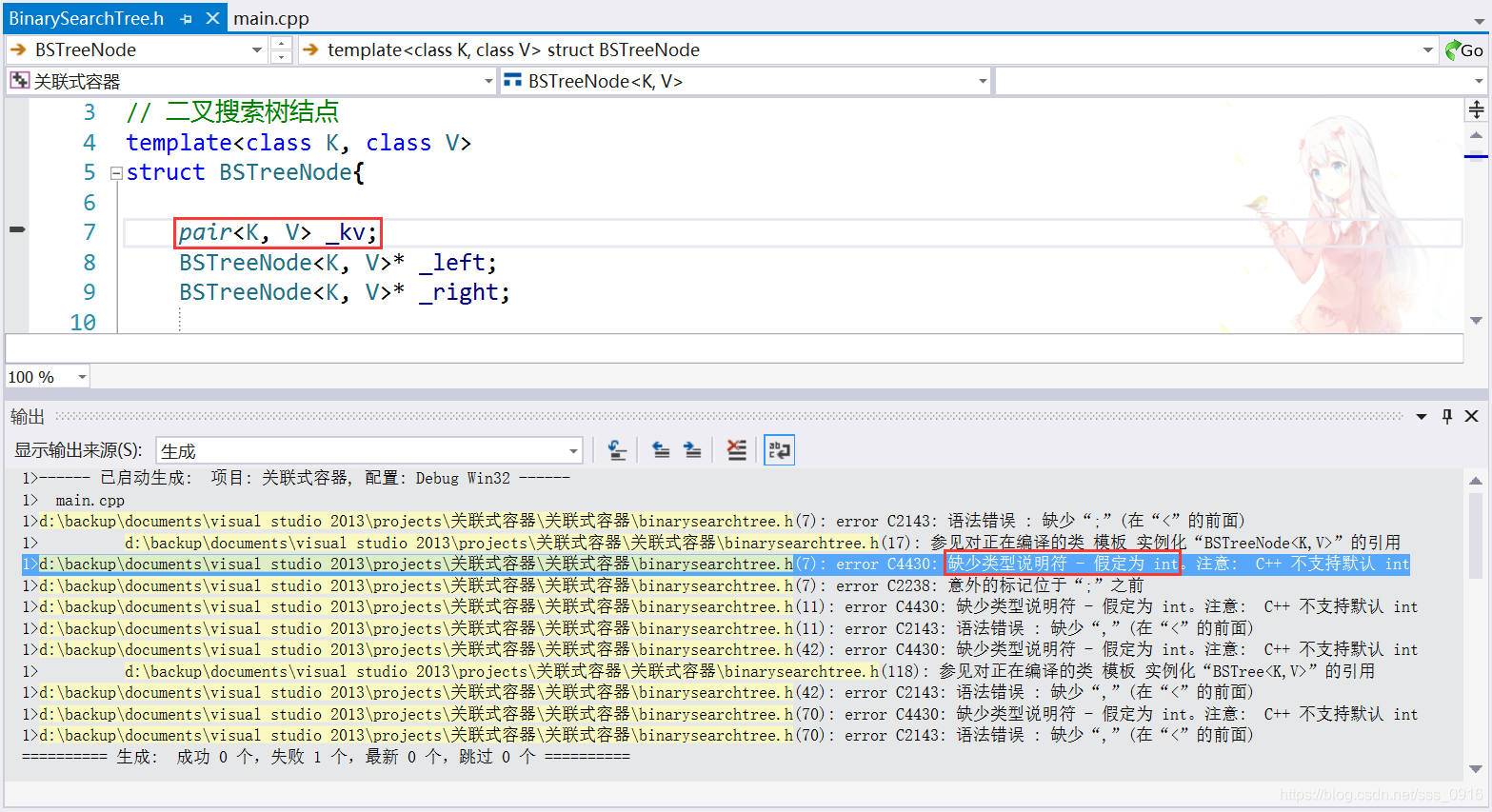
二叉搜索树结点中pair _kv;语句报错，缺少范例分析符。错误缘故原由临时不详。
办理方案如下：
将第3行和第4行互换一下，就可以了O(∩_∩)O哈哈~。

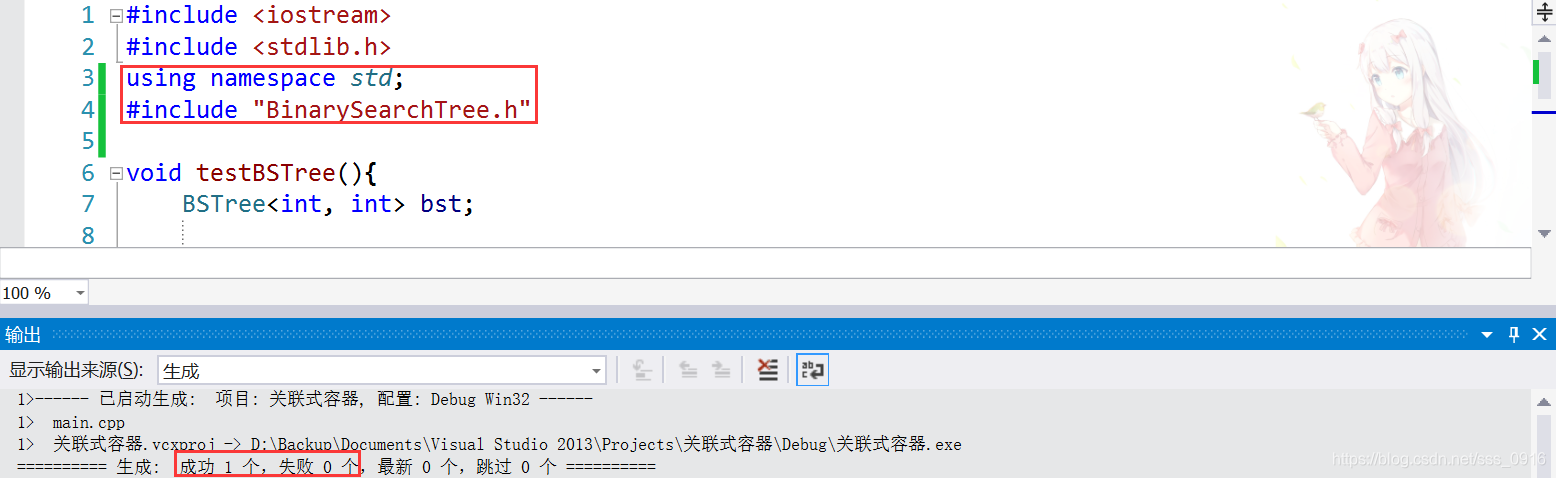
BinarySearchTree.h：

#pragma once

// 二叉搜索树结点
template<class K, class V>
struct BSTreeNode{

	pair<K, V> _kv;
	BSTreeNode<K, V>* _left;
	BSTreeNode<K, V>* _right;

	BSTreeNode(const pair<K, V>& kv)
		: _left(nullptr)
		, _right(nullptr)
		, _kv(kv)
	{}

};

// 二叉搜索树
template<class K, class V>
class BSTree{
	typedef BSTreeNode<K, V> Node;

public:
	BSTree()
		: _root(nullptr)
	{}

	~BSTree(){
		// 二叉搜索树的开释
		_release(_root);
	}

	// 二叉树的中序遍历
	void inorder(){
		_inorder(_root);

		cout << endl;
	}

	// 二叉搜索树的查找
	Node* find(const K& key){
		return _find(key);
	}

	// 二叉搜索树的插入
	bool insert(const pair<K, V>& kv){
		return _insert(kv);
	}

	// 二叉搜索树的删除
	bool remove(const K& key){
		return _remove(key);
	}

private:
	// 开释
	void _release(Node* root){
		// 该树非空
		if (root){
			// 生存左右孩子
			Node* left = root->_left;
			Node* right = root->_right;

			// 开释根
			delete root;

			// 左树非空，开释左树
			if (left){
				_release(left);
			}

			// 右树非空，开释右树
			if (right){
				_release(right);
			}
		}
	}

	// 中序遍历
	void _inorder(Node* root){
		// 递归出口
		if (root == nullptr){
			return;
		}

		_inorder(root->_left);
		cout << root->_kv.first << " ";
		_inorder(root->_right);
	}

	// 查找
	Node* _find(const K& key){
		Node* cur = _root;

		while (cur != nullptr){
			// 比根结点大，去右子树找
			if (key > cur->_kv.first){
				cur = cur->_right;
			}
			// 比根结点小，去左子树找
			else if (key < cur->_kv.first){
				cur = cur->_left;
			}
			// 相称
			else{
				break;
			}
		}

		return cur;
	}

	// 插入
	bool _insert(const pair<K, V>& kv){
		// 树为空
		if (_root == nullptr){
			_root = new Node(kv);

			return true;
		}
		// 树不为空
		else{
			Node* cur = _root;
			// 生存父节点
			Node* parent = nullptr;

			while (cur != nullptr){
				parent = cur;

				// 比根结点大，去右子树
				if (kv.first > cur->_kv.first){
					cur = cur->_right;
				}
				// 比根结点小，去左子树
				else if (kv.first < cur->_kv.first){
					cur = cur->_left;
				}
				// 和根结点一样，已存在，插入失败
				else{
					return false;
				}
			}

			// 新插入结点
			cur = new Node(kv);

			// 比双亲结点大，插入到右树
			if (kv.first > parent->_kv.first){
				parent->_right = cur;
			}
			// 比双亲结点小，插入到左树
			else{
				parent->_left = cur;
			}

			return true;
		}
	}

	// 删除
	bool _remove(const K& key){
		Node* cur = _root;
		// 生存父结点
		Node* parent = nullptr;

		while (cur != nullptr){
			// 比根结点大，右树找
			if (key > cur->_kv.first){
				parent = cur;
				cur = cur->_right;
			}
			// 比根结点小，左树找
			else if (key < cur->_kv.first){
				parent = cur;
				cur = cur->_left;
			}
			// 找到了
			else{
				// 该节点左树为空
				if (cur->_left == nullptr){
					// 该节点为根结点
					if (parent == nullptr){
						_root = cur->_right;
					}
					else{
						// 该节点在父结点的右树
						if (cur->_kv.first > parent->_kv.first){
							parent->_right = cur->_right;
						}
						// 该节点在父结点的左树
						else{
							parent->_left = cur->_right;
						}
					}
				}
				// 该节点右树为空
				else if (cur->_right == nullptr){
					// 该节点为根结点
					if (parent == nullptr){
						_root = cur->_left;
					}

					// 该节点在父结点的右树
					if (cur->_kv.first > parent->_kv.first){
						parent->_right = cur->_left;
					}
					// 该节点在父结点的右树
					else{
						parent->_left = cur->_right;
					}
				}
				// 该节点左右树都不为空
				else{
					// 右树中探求更换结点
					Node* replace = cur->_right;
					// 生存更换结点的父结点
					Node* rparent = cur;

					// 探求最左结点，即右树中的最小值
					while (replace->_left){
						rparent = replace;
						replace = replace->_left;
					}

					cur->_kv = replace->_kv;
					cur = replace;

					// 判断replace是否有左树
					// replace有左树
					if (rparent->_left == replace){
						// 将更换结点的右树连到更换结点的父结点的左树
						rparent->_left = replace->_right;
					}
					// replace没有左树
					else{
						// 将更换结点的右树连到更换结点的父结点的右树
						rparent->_right = replace->_right;
					}
				}

				// 删除更换结点
				delete cur;

				return true;
			}
		}
		return false;
	}

private:
	Node* _root;
};